Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
- q→=−ϰgrad(T),{\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}
где q→{\displaystyle {\vec {q}}}
— вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ{\displaystyle \varkappa }
— коэффициент теплопроводности (удельная теплопроводность), T{\displaystyle T}
— температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad(T){\displaystyle \mathrm {grad} (T)}
(то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
-
P=−ϰSΔTl,{\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},}
[Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]
где P{\displaystyle P}
— полная мощность тепловых потерь, S{\displaystyle S}
— площадь сечения параллелепипеда, ΔT{\displaystyle \Delta T}
— перепад температур граней, l{\displaystyle l}
— длина параллелепипеда, то есть расстояние между гранями.
Связь с электропроводностью
Связь коэффициента теплопроводности ϰ{\displaystyle \varkappa }
с удельной электрической проводимостью σ{\displaystyle \sigma }
в металлах устанавливает закон Видемана — Франца:
- ϰσ=π23(ke)2T,{\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,}
- где k{\displaystyle k}
— постоянная Больцмана; -
e{\displaystyle e}
— заряд электрона; -
T{\displaystyle T}
— абсолютная температура.
Коэффициент теплопроводности газов
В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]
- ϰ∼13ρcvλv¯,{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}
где ρ{\displaystyle \rho }
— плотность газа, cv{\displaystyle c_{v}}
— удельная теплоёмкость при постоянном объёме, λ{\displaystyle \lambda }
— средняя длина свободного пробега молекул газа, v¯{\displaystyle {\bar {v}}}
— средняя тепловая скорость. Эта же формула может быть записана как[3]
- ϰ=ik3π3/2d2RTμ,{\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}
где i{\displaystyle i}
— сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5{\displaystyle i=5}
, для одноатомного i=3{\displaystyle i=3}
), k{\displaystyle k}
— постоянная Больцмана, μ{\displaystyle \mu }
— молярная масса, T{\displaystyle T}
— абсолютная температура, d{\displaystyle d}
— эффективный (газокинетический) диаметр молекул, R{\displaystyle R}
— универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ∼13ρcvlv¯∝P{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P}
, где l{\displaystyle l}
— размер сосуда, P{\displaystyle P}
— давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Таблица теплопроводности
| Материал | Плотность, кг/м3 | Теплопроводность, Вт/(м*С) | Паропроницаемость, Мг/(м*ч*Па) |
Эквивалентная1(при сопротивлении теплопередаче = 4,2м2*С/Вт) толщина, м | Эквивалентная2(при сопротивление паропроницанию =1,6м2*ч*Па/мг) толщина, м |
| Железобетон | 2500 | 1.69 | 0.03 | 7.10 | 0.048 |
| Бетон | 2400 | 1.51 | 0.03 | 6.34 | 0.048 |
| Керамзитобетон | 1800 | 0.66 | 0.09 | 2.77 | 0.144 |
| Керамзитобетон | 500 | 0.14 | 0.30 | 0.59 | 0.48 |
| Кирпич красный глиняный | 1800 | 0.56 | 0.11 | 2.35 | 0.176 |
| Кирпич, силикатный | 1800 | 0.70 | 0.11 | 2.94 | 0.176 |
| Кирпич керамический пустотелый (брутто1400) | 1600 | 0.41 | 0.14 | 1.72 | 0.224 |
| Кирпич керамический пустотелый (брутто 1000) | 1200 | 0.35 | 0.17 | 1.47 | 0.272 |
| Пенобетон | 1000 | 0.29 | 0.11 | 1.22 | 0.176 |
| Пенобетон | 300 | 0.08 | 0.26 | 0.34 | 0.416 |
| Гранит | 2800 | 3.49 | 0.008 | 14.6 | 0.013 |
| Мрамор | 2800 | 2.91 | 0.008 | 12.2 | 0.013 |
| Сосна, ель поперек волокна | 500 | 0.09 | 0.06 | 0.38 | 0.096 |
| Дуб поперек волокна | 700 | 0.10 | 0.05 | 0.42 | 0.08 |
| Сосна, ель вдоль волокна | 500 | 0.18 | 0.32 | 0.75 | 0.512 |
| Дуб вдоль волокна | 700 | 0.23 | 0.30 | 0.96 | 0.48 |
| Фанера | 600 | 0.12 | 0.02 | 0.50 | 0.032 |
| ДСП | 1000 | 0.15 | 0.12 | 0.63 | 0.192 |
| Пакля | 150 | 0.05 | 0.49 | 0.21 | 0.784 |
| Гипсокартон | 800 | 0.15 | 0.075 | 0.63 | 0.12 |
| Картон облицовочный | 1000 | 0.18 | 0.06 | 0.75 | 0.096 |
| Минвата | 200 | 0.070 | 0.49 | 0.30 | 0.784 |
| Минвата | 100 | 0.056 | 0.56 | 0.23 | 0.896 |
| Минвата | 50 | 0.048 | 0.60 | 0.20 | 0.96 |
| Пенополистирол экструдированный | 33 | 0.031 | 0.013 | 0.13 | 0.021 |
| Пенополистирол экструдированный | 45 | 0.036 | 0.013 | 0.13 | 0.021 |
| Пенополистирол | 150 | 0.05 | 0.05 | 0.21 | 0.08 |
| Пенополистирол | 100 | 0.041 | 0.05 | 0.17 | 0.08 |
| Пенополистирол | 40 | 0.038 | 0.05 | 0.16 | 0.08 |
| ПВХ | 125 | 0.052 | 0.23 | 0.22 | 0.368 |
| Пенополиуретан | 80 | 0.041 | 0.05 | 0.17 | 0.08 |
| Пенополиуретан | 60 | 0.035 | 0.0 | 0.15 | 0.08 |
| Пенополиуретан | 40 | 0.029 | 0.05 | 0.12 | 0.08 |
| Пенополиуретан | 30 | 0.020 | 0.05 | 0.09 | 0.08 |
| Керамзит | 800 | 0.18 | 0.21 | 0.75 | 0.336 |
| Керамзит | 200 | 0.10 | 0.26 | 0.42 | 0.416 |
| Песок | 1600 | 0.35 | 0.17 | 1.47 | 0.272 |
| Пеностекло | 400 | 0.11 | 0.02 | 0.46 | 0.032 |
| Пеностекло | 200 | 0.07 | 0.03 | 0.30 | 0.048 |
| АЦП | 1800 | 0.35 | 0.03 | 1.47 | 0.048 |
| Битум | 1400 | 0.27 | 0.008 | 1.13 | 0.013 |
| Полиуретановая мастика | 1400 | 0.25 | 0.00023 | 1.05 | 0.00036 |
| Полимочевина | 1100 | 0.21 | 0.00023 | 0.88 | 0.00054 |
| Рубероид, пергамин | 600 | 0.17 | 0.001 | 0.71 | 0.0016 |
| Полиэтилен | 1500 | 0.30 | 0.00002 | 1.26 | 0.000032 |
| Асфальтобетон | 2100 | 1.05 | 0.008 | 4.41 | 0.0128 |
| Линолеум | 1600 | 0.33 | 0.002 | 1.38 | 0.0032 |
| Сталь | 7850 | 58 | 0 | 243 | 0 |
| Алюминий | 2600 | 221 | 0 | 928 | 0 |
| Медь | 8500 | 407 | 0 | 1709 | 0 |
| Стекло | 2500 | 0.76 | 0 | 3.19 | 0 |
Понятие теплопроводности
Теплопроводность – это такое физическое свойство материала, при которой тепловая энергия внутри тела переходит от самой горячей его части к более холодной. Значение показателя теплопроводности показывает степень потери тепла жилыми помещениями. Зависит от следующих факторов:
- плотности предмета: возрастает с её увеличением;
- структуры: к примеру, дерево с поперечными волокнами отличается большим термическим сопротивлением, чем с продольными;
- пористости: чем выше значение, тем меньше средняя плотность;
- характера пустот и пор: материалы с сообщающимися порами имеют большую теплопроводность, с закрытыми мелкозернистыми порами – меньшую;
- влажности: сухие предметы менее теплопроводны;
- температуры – теплообмен уменьшается с её увеличением;
- давления – показатель увеличивается с ростом давления.
Количественно оценить свойство предметов пропускать тепловую энергию можно посредством коэффициента теплопроводности
Очень важно сделать грамотный выбор строительных материалов, утеплителя для достижения наибольшего сопротивления теплопередачи. Просчёты или неразумная экономия в будущем могут привести к ухудшению микроклимата в помещении, сырости в здании, мокрым стенам, душным комнатам
А главное – к большим расходам на отопление.
Для сравнения ниже представлена и веществ.
Таблица 1
| Материалы и вещества | алюминий | сталь | сталь нержавеющая | бетон | воздух | вода | ДСП | рубероид | картон | резина | полиэтилен | стекло |
| Коэффициент теплопроводности | 221 | 58 | 17,5 | 1,5 | 0,02 | 0,6 | 0,15 | 0,17 | 0,18 | 0,04 | 0,3 | 0,7 |
Самые высокие значения имеют металлы, низкие – теплоизоляционные предметы.
Коэффициент теплопроводности.
Количество тепла, которое проходит через стены (а по научному – интенсивность теплопередачи за счет теплопроводности) зависит от разности температур (в доме и на улице), от площади стен и теплопроводности материала, из которого сделаны эти стены.
Для количественной оценки теплопроводности существует коэффициент теплопроводности материалов. Этот коэффициент отражает свойство вещества проводить тепловую энергию. Чем больше значение коэффициента теплопроводности материала, тем лучше он проводит тепло. Если мы собираемся утеплять дом, то надо выбирать материалы с небольшим значением этого коэффициента. Чем он меньше, тем лучше. Сейчас в качестве материалов для утепления зданий наибольшее распространение получили утеплители из минеральной ваты, и различных пенопластов. Набирает популярность новый материал с улучшенными теплоизоляционными качествами – Неопор.
Коэффициент теплопроводности материалов обозначается буквой ? (греческая строчная буква лямбда) и выражается в Вт/(м2*К). Это означает, что если взять стену из кирпича, с коэффициентом теплопроводности 0,67 Вт/(м2*К), толщиной 1 метр и площадью 1 м2., то при разнице температур в 1 градус, через стену будет проходить 0,67 ватта тепловой энергии. Если разница температур будет 10 градусов, то будет проходить уже 6,7 ватта. А если при такой разнице температур стену сделать 10 см, то потери тепла будут уже 67 ватт. Подробней о методике расчета теплопотерь зданий можно посмотреть здесь.
Следует отметить, что значения коэффициента теплопроводности материалов указываются для толщины материала в 1 метр. Чтобы определить теплопроводность материала для любой другой толщины, надо коэффициент теплопроводности разделить на нужную толщину, выраженную в метрах.
В строительных нормах и расчетах часто используется понятие “тепловое сопротивление материала”. Это величина обратная теплопроводности. Если, на пример, теплопроводность пенопласта толщиной 10 см – 0,37 Вт/(м2*К), то его тепловое сопротивление будет равно 1 / 0,37 Вт/(м2*К) = 2,7 (м2*К)/Вт.
Примеры решения задач
ПРИМЕР 1
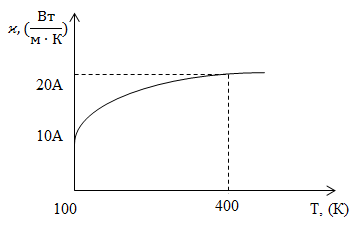
| Задание | Каким будет коэффициент теплопроводности воздуха, если его давление равно , температура ? Диаметр молекулы считать равным . Постройте график зависимости коэффициента теплопроводности от температуры газа. |
| Решение | За основу решения задачи примем формулу расчета теплопроводности газа:
Средняя длина свободного пробега молекулы может быть найдена при и известных макропараметрах, характеризующих газ (p, V, T) как:
Среднюю скорость теплового движения молекул примем равной:
Плотность газа найдем, используя уравнение Менделеева — Клайперона:
зная, что
Используя формулы (1.4) и (1.5), получим:
Теплоемкость газа () при постоянном объеме равна:
где число степеней свободы молекулы воздуха будем считать равным 5. Используя выражения (1.2), (1.3), (1.6) и (1.7) подставляя в формулу (1.1) получаем:
Мы получили функцию зависимости коэффициента теплопроводности для газа вида:
Изобразим ее на графике (рис.1).
Рис. 1 |
| Ответ |
ПРИМЕР 2
| Задание | Каким будет коэффициент диффузии двухатомного газа (D), если известны для него: коэффициент теплопроводности (), его объем V, N — количество молекул данного газа? |
| Решение | Используем выражение коэффициента теплопроводности из кинетической теории:
Коэффициент диффузии имеет выражение:
Из формул (2.1) и (2.2) видно, что:
Теплоемкость газа в изохорном процессе равна
Найдем плотность газа, зная, что
Учитывая формулы (2.4) и (2.5) окончательно получаем для коэффициента диффузии:
где — постоянная Больцмана (). |
| Ответ |
От чего зависит теплопроводность
Значения данной величины могут зависеть от нескольких факторов. Например, коэффициент теплопроводности, о котором мы поговорим отдельно, влажность строительного сырья, плотность и так далее.
- Материалы, имеющие высокие показатели плотности, имеют, в свою очередь, и высокую способность к теплоотдаче, за счёт плотного скопления молекул внутри вещества. Пористые материалы, наоборот, будут нагреваться и остывать медленнее.
- На теплопередачу оказывает влияние и влажность материалов. Если материалы промокнут, то их теплоотдача возрастёт.
- Также, сильно влияет на этот показатель структура материала. Например, дерево с поперечными и продольными волокнами будет иметь разные значения теплопроводности.
- Показатель изменяется и при изменениях таких параметров, как давление и температура. С ростом температуры он увеличивается, а с ростом давления, наоборот – уменьшается.
Расчёт толщины утеплителя
 Из вышеприведённых таблиц мы видим, насколько могут отличаться коэффициенты проводимости тепла у разных материалов. Для расчёта теплосопротивления будущей стены, существует нехитрая формула, которая связывает толщину утеплителя и коэффициент его теплопроводности.
Из вышеприведённых таблиц мы видим, насколько могут отличаться коэффициенты проводимости тепла у разных материалов. Для расчёта теплосопротивления будущей стены, существует нехитрая формула, которая связывает толщину утеплителя и коэффициент его теплопроводности.
R = p / k , где R -показатель теплосопротивления, p -толщина слоя, k – коэффициент.
Из этой формулы несложно выделить и формулу расчёта толщины слоя утеплителя для требуемого теплосопротивления. P = R * k . Значение теплосопротивление разное для каждого региона. Для этих значений тоже существует специальная таблица, где их и можно посмотреть при расчёте толщины утеплителя.
Теперь приведём примеры некоторых наиболее популярных утеплителей и их технических характеристик.
- Гипсокартон. Гиспокартон является очень популярным строительным материалом и часто применяется для утепления стен изнутри. Имеет плотность от 500 до 900 кг/м3, коэффициент теплопроводности от 0,12 до 0,2 Вт/кг*С в зависимости от разновидности гипсокартона.
- Стекловата. Довольно популярный утеплитель. Сейчас применяется значительно реже, чем раньше. Плотность стекловаты 15-45 кг / м3 а коэффициент – 0,38-0,46 Вт / кг*С 1.
- Существует ещё большое количество различных утеплителей для дома, как применяемых, так и не очень. При выборе нужно иметь в виду свои экономические возможности и результаты расчёта по вышеприведённым формулам.
Конструкционные материалы и их показатели
Для строительства зданий используют материалы с низким коэффициентом теплопроводности. Наиболее популярными являются:
- Бетон. Его теплопроводность находится в пределах 1,29-1,52Вт/м*К. Точное значение зависит от консистенции раствора. На этот показатель также влияет плотность исходного материала, которая составляет 500-2500 кг/м3. Используют данный материал в виде раствора для фундаментов, в виде блоков – для возведения стен и фундамента.
- Железобетон, значение теплопроводности которого составляет 1,68Вт/м*К. Плотность материала достигает 2400-2500 кг/м3.
- Древесина, издревле использующаяся как строительный материал. Ее плотность и теплопроводность в зависимости от породы составляют 150-2100 кг/м3 и 0,2-0,23Вт/м*К соответственно.
Еще один популярный строительный материал – кирпич. В зависимости от состава он обладает следующими показателями:
- саманный (изготовленный из глины): 0,1-0,4 Вт/м*К;
- керамический (изготовленный методом обжига): 0,35-0,81 Вт/м*К;
- силикатный (из песка с добавлением извести): 0,82-0,88 Вт/м*К.
Закон теплопроводности Фурье
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:
- q→=−ϰgrad(T),{\displaystyle {\vec {q}}=-\varkappa \,\mathrm {grad} (T),}
где q→{\displaystyle {\vec {q}}} — вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, ϰ{\displaystyle \varkappa } — коэффициент теплопроводности (удельная теплопроводность), T{\displaystyle T} — температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad(T){\displaystyle \mathrm {grad} (T)} (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.[1]
В интегральной форме это же выражение запишется так (если речь идёт о стационарном потоке тепла от одной грани параллелепипеда к другой):
- P=−ϰSΔTl,{\displaystyle P=-\varkappa {\frac {S\Delta T}{l}},} [Вт/(м·К) · (м2·К)/м = Вт/(м·К) · (м·К) = Вт]
где P{\displaystyle P} — полная мощность тепловых потерь, S{\displaystyle S} — площадь сечения параллелепипеда, ΔT{\displaystyle \Delta T} — перепад температур граней, l{\displaystyle l} — длина параллелепипеда, то есть расстояние между гранями.
Связь с электропроводностью
Связь коэффициента теплопроводности ϰ{\displaystyle \varkappa } с удельной электрической проводимостью σ{\displaystyle \sigma } в металлах устанавливает закон Видемана — Франца:
- ϰσ=π23(ke)2T,{\displaystyle {\frac {\varkappa }{\sigma }}={\frac {\pi ^{2}}{3}}\left({\frac {k}{e}}\right)^{2}T,}
- где k{\displaystyle k} — постоянная Больцмана;
- e{\displaystyle e} — заряд электрона;
- T{\displaystyle T} — абсолютная температура.
Коэффициент теплопроводности газов
В газах коэффициент теплопроводности может быть найден по приближённой формуле[2]
- ϰ∼13ρcvλv¯,{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}\lambda {\bar {v}},}
где ρ{\displaystyle \rho } — плотность газа, cv{\displaystyle c_{v}} — удельная теплоёмкость при постоянном объёме, λ{\displaystyle \lambda } — средняя длина свободного пробега молекул газа, v¯{\displaystyle {\bar {v}}} — средняя тепловая скорость. Эта же формула может быть записана как[3]
- ϰ=ik3π3/2d2RTμ,{\displaystyle \varkappa ={\frac {ik}{3\pi ^{3/2}d^{2}}}{\sqrt {\frac {RT}{\mu }}},}
где i{\displaystyle i} — сумма поступательных и вращательных степеней свободы молекул (для двухатомного газа i=5{\displaystyle i=5}, для одноатомного i=3{\displaystyle i=3}), k{\displaystyle k} — постоянная Больцмана, μ{\displaystyle \mu } — молярная масса, T{\displaystyle T} — абсолютная температура, d{\displaystyle d} — эффективный (газокинетический) диаметр молекул, R{\displaystyle R} — универсальная газовая постоянная. Из формулы видно, что наименьшей теплопроводностью обладают тяжелые одноатомные (инертные) газы, наибольшей — легкие многоатомные (что подтверждается практикой, максимальная теплопроводность из всех газов — у водорода, минимальная — у радона, из нерадиоактивных газов — у ксенона).
Теплопроводность в сильно разреженных газах
Приведённое выше выражение для коэффициента теплопроводности в газах не зависит от давления. Однако если газ сильно разрежен, то длина свободного пробега определяется не столкновениями молекул друг с другом, а их столкновениями со стенками сосуда. Состояние газа, при котором длина свободного пробега молекул ограничивается размерами сосуда называют высоким вакуумом. При высоком вакууме теплопроводность убывает пропорционально плотности вещества (то есть пропорциональна давлению в системе): ϰ∼13ρcvlv¯∝P{\displaystyle \varkappa \sim {\frac {1}{3}}\rho c_{v}l{\bar {v}}\propto P}, где l{\displaystyle l} — размер сосуда, P{\displaystyle P} — давление.
Таким образом коэффициент теплопроводности вакуума тем ближе к нулю, чем глубже вакуум. Это связано с низкой концентрацией в вакууме материальных частиц, способных переносить тепло. Тем не менее, энергия в вакууме передаётся с помощью излучения. Поэтому, например, для уменьшения теплопотерь стенки делают двойными, серебрят (такая поверхность лучше отражает излучение), а воздух между ними откачивают.
Коэффициенты теплопроводности различных веществ

Цветок на куске аэрогеля над горелкой Бунзена
| Материал | Теплопроводность, Вт/(м·K) |
|---|---|
| Графен | 4840 ± 440 — 5300 ± 480 |
| Алмаз | 1001—2600 |
| Графит | 278,4—2435 |
| Арсенид бора[en] | 200—2000 |
| Карбид кремния | 490 |
| Серебро | 430 |
| Медь | 401 |
| Оксид бериллия | 370 |
| Золото | 320 |
| Алюминий | 202—236 |
| Нитрид алюминия | 200 |
| Нитрид бора | 180 |
| Кремний | 150 |
| Латунь | 97—111 |
| Хром | 107 |
| Железо | 92 |
| Платина | 70 |
| Олово | 67 |
| Оксид цинка | 54 |
| Сталь нелегированная | 47—58 |
| Свинец | 35,3 |
| Сталь нержавеющая (аустенитная) [6] | 15 |
| Кварц | 8 |
| Термопасты высокого качества | 5—12 (на основе соединений углерода) |
| Гранит | 2,4 |
| Бетон сплошной | 1,75 |
| Бетон на гравии или щебне из природного камня | 1,51 |
| Базальт | 1,3 |
| Стекло | 1—1,15 |
| Термопаста КПТ-8 | 0,7 |
| Бетон на песке | 0,7 |
| Вода при нормальных условиях | 0,6 |
| Кирпич строительный | 0,2—0,7 |
| Силиконовое масло | 0,16 |
| Пенобетон | 0,05—0,3 |
| Газобетон | 0,1—0,3 |
| Древесина | 0,15 |
| Нефтяные масла | 0,12 |
| Свежий снег | 0,10—0,15 |
| Пенополистирол (горючесть Г1) | 0,038—0,052 |
| Экструдированный пенополистирол (горючесть Г3 и Г4) | 0,029—0,032 |
| Стекловата | 0,032—0,041 |
| Каменная вата | 0,034—0,039 |
| Воздух (300 K, 100 кПа) | 0,022 |
| Аэрогель | 0,017 |
| Аргон (273—320 K, 100 кПа) | 0,017 |
| Аргон (240—273 K, 100 кПа) | 0,015 |
| Вакуум (абсолютный) | 0 (строго) |
Также нужно учитывать передачу тепла из-за конвекции молекул и излучения. Например, при полной нетеплопроводности вакуума, тепловая энергия передаётся излучением (Солнце, инфракрасные теплогенераторы). В газах и жидкостях происходит перемешивание разнотемпературных слоёв естественным путём или искусственно (примеры принудительного перемешивания — фены, естественного — электрочайники). Также в конденсированных средах возможно «перепрыгивание» из одного твердого тела в другое через субмикронные зазоры, что способствует распространению звуковых волн и тепловой энергии, даже если зазоры представляют собой идеальный вакуум.
Понятие теплопроводности на практике
Теплопроводность учитывается на этапе проектирования здания
При этом берется во внимание способность материалов удерживать тепло. Благодаря их правильному подбору жильцам внутри помещения всегда будет комфортно
Во время эксплуатации будут существенно экономиться денежные средства на отопление.
Утепление на стадии проектирования является оптимальным, но не единственным решением. Не составляет трудности утеплить уже готовое здание путем проведения внутренних или наружных работ. Толщина слоя изоляции будет зависеть от выбранных материалов. Отдельные из них (к примеру, дерево, пенобетон) могут в некоторых случаях использоваться без дополнительного слоя термоизоляции. Главное, чтобы их толщина превышала 50 сантиметров.
Особенное внимание следует уделить утеплению кровли, оконных и дверных проемов, пола. Сквозь эти элементы уходит больше всего тепла. Зрительно это можно увидеть на фотографии в начале статьи.
Обобщения закона Фурье
Следует отметить, что закон Фурье не учитывает инерционность процесса теплопроводности, то есть в данной модели изменение температуры в какой-то точке мгновенно распространяется на всё тело. Закон Фурье неприменим для описания высокочастотных процессов (и, соответственно, процессов, чьё разложение в ряд Фурье имеет значительные высокочастотные гармоники). Примерами таких процессов являются распространение ультразвука, ударные волны и т. п. Инерционность в уравнения переноса первым ввел Максвелл[4], а в 1948 году Каттанео был предложен вариант закона Фурье с релаксационным членом:
- τ∂q∂t=−(q+ϰ∇T).{\displaystyle \tau {\frac {\partial \mathbf {q} }{\partial t}}=-\left(\mathbf {q} +\varkappa \,\nabla T\right).}
Если время релаксации τ{\displaystyle \tau } пренебрежимо мало, то это уравнение переходит в закон Фурье.
Ваш дом может сохранят тепло
Достижения строительной индустрии, динамика развития которой поражает, дают нам возможность существенно экономить на содержании архитектурных сооружений. Сегодня можно построить не просто надежное, безопасное и эстетически привлекательно здание, но и придать ему такие свойства как поддержание определенного микроклимата и сохранение тепла. Для этого еще на этапе разработки проекта конструкции необходимо задействовать материалы, коэффициент теплопроводности которых соответствует нашим желаниям.
Отсутствие теплоизоляции дома скажется на температуре воздуха внутри помещения
Таблица теплопроводности теплоизоляционных материалов
Чтобы в доме было проще сохранять тепло зимой и прохладу летом, теплопроводность стен, пола и кровли должна быть не менее определенной цифры, которая рассчитывается для каждого региона. Состав «пирога» стен, пола и потолка, толщина материалов берутся с таким учетом чтобы суммарная цифра была не меньше (а лучше — хоть немного больше) рекомендованной для вашего региона.
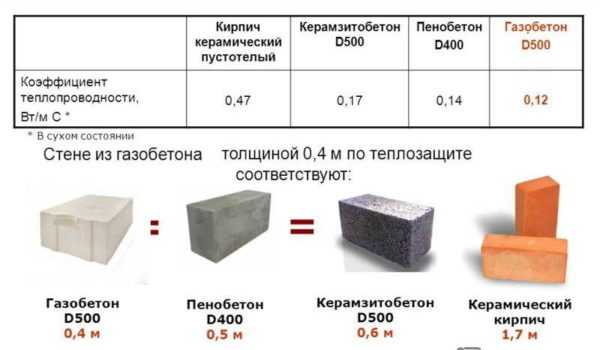
Коэффициент теплопередачи материалов современных строительных материалов для ограждающих конструкций
При выборе материалов надо учесть, что некоторые из них (не все) в условиях повышенной влажности проводят тепло гораздо лучше. Если при эксплуатации возможно возникновение такой ситуации на продолжительный срок, в расчетах используют теплопроводность для этого состояния. Коэффициенты теплопроводности основных материалов, которые используются для утепления, приведены в таблице.
| Наименование материала | Коэффициент теплопроводности Вт/(м·°C) | ||
|---|---|---|---|
| В сухом состоянии | При нормальной влажности | При повышенной влажности | |
| Войлок шерстяной | 0,036-0,041 | 0,038-0,044 | 0,044-0,050 |
| Каменная минеральная вата 25-50 кг/м3 | 0,036 | 0,042 | 0,,045 |
| Каменная минеральная вата 40-60 кг/м3 | 0,035 | 0,041 | 0,044 |
| Каменная минеральная вата 80-125 кг/м3 | 0,036 | 0,042 | 0,045 |
| Каменная минеральная вата 140-175 кг/м3 | 0,037 | 0,043 | 0,0456 |
| Каменная минеральная вата 180 кг/м3 | 0,038 | 0,045 | 0,048 |
| Стекловата 15 кг/м3 | 0,046 | 0,049 | 0,055 |
| Стекловата 17 кг/м3 | 0,044 | 0,047 | 0,053 |
| Стекловата 20 кг/м3 | 0,04 | 0,043 | 0,048 |
| Стекловата 30 кг/м3 | 0,04 | 0,042 | 0,046 |
| Стекловата 35 кг/м3 | 0,039 | 0,041 | 0,046 |
| Стекловата 45 кг/м3 | 0,039 | 0,041 | 0,045 |
| Стекловата 60 кг/м3 | 0,038 | 0,040 | 0,045 |
| Стекловата 75 кг/м3 | 0,04 | 0,042 | 0,047 |
| Стекловата 85 кг/м3 | 0,044 | 0,046 | 0,050 |
| Пенополистирол (пенопласт, ППС) | 0,036-0,041 | 0,038-0,044 | 0,044-0,050 |
| Экструдированный пенополистирол (ЭППС, XPS) | 0,029 | 0,030 | 0,031 |
| Пенобетон, газобетон на цементном растворе, 600 кг/м3 | 0,14 | 0,22 | 0,26 |
| Пенобетон, газобетон на цементном растворе, 400 кг/м3 | 0,11 | 0,14 | 0,15 |
| Пенобетон, газобетон на известковом растворе, 600 кг/м3 | 0,15 | 0,28 | 0,34 |
| Пенобетон, газобетон на известковом растворе, 400 кг/м3 | 0,13 | 0,22 | 0,28 |
| Пеностекло, крошка, 100 — 150 кг/м3 | 0,043-0,06 | ||
| Пеностекло, крошка, 151 — 200 кг/м3 | 0,06-0,063 | ||
| Пеностекло, крошка, 201 — 250 кг/м3 | 0,066-0,073 | ||
| Пеностекло, крошка, 251 — 400 кг/м3 | 0,085-0,1 | ||
| Пеноблок 100 — 120 кг/м3 | 0,043-0,045 | ||
| Пеноблок 121- 170 кг/м3 | 0,05-0,062 | ||
| Пеноблок 171 — 220 кг/м3 | 0,057-0,063 | ||
| Пеноблок 221 — 270 кг/м3 | 0,073 | ||
| Эковата | 0,037-0,042 | ||
| Пенополиуретан (ППУ) 40 кг/м3 | 0,029 | 0,031 | 0,05 |
| Пенополиуретан (ППУ) 60 кг/м3 | 0,035 | 0,036 | 0,041 |
| Пенополиуретан (ППУ) 80 кг/м3 | 0,041 | 0,042 | 0,04 |
| Пенополиэтилен сшитый | 0,031-0,038 | ||
| Вакуум | 0 | ||
| Воздух +27°C. 1 атм | 0,026 | ||
| Ксенон | 0,0057 | ||
| Аргон | 0,0177 | ||
| Аэрогель (Aspen aerogels) | 0,014-0,021 | ||
| Шлаковата | 0,05 | ||
| Вермикулит | 0,064-0,074 | ||
| Вспененный каучук | 0,033 | ||
| Пробка листы 220 кг/м3 | 0,035 | ||
| Пробка листы 260 кг/м3 | 0,05 | ||
| Базальтовые маты, холсты | 0,03-0,04 | ||
| Пакля | 0,05 | ||
| Перлит, 200 кг/м3 | 0,05 | ||
| Перлит вспученный, 100 кг/м3 | 0,06 | ||
| Плиты льняные изоляционные, 250 кг/м3 | 0,054 | ||
| Полистиролбетон, 150-500 кг/м3 | 0,052-0,145 | ||
| Пробка гранулированная, 45 кг/м3 | 0,038 | ||
| Пробка минеральная на битумной основе, 270-350 кг/м3 | 0,076-0,096 | ||
| Пробковое покрытие для пола, 540 кг/м3 | 0,078 | ||
| Пробка техническая, 50 кг/м3 | 0,037 |
Часть информации взята нормативов, которые прописывают характеристики определенных материалов (СНиП 23-02-2003, СП 50.13330.2012, СНиП II-3-79* (приложение 2)). Те материал, которые не прописаны в стандартах, найдены на сайтах производителей
Так как стандартов нет, у разных производителей они могут значительно отличаться, потому при покупке обращайте внимание на характеристики каждого покупаемого материала.